>
JUSTIFICACIÓN
Se nos ha pedido la elaboración de un blog cuyo objetivo principal es la explicación del tema propuesto del profesor a nosotros, alumnos, a continuación expondré el tema correspondiente asignado que espero sea de su entero entendimiento e interés.
Llevar a cabo el proyecto dado por el docente como responsabilidad propia y otra nueva forma de aprendizaje. Especifico: Lograr explicar a los estudiantes de una forma mas dinámica utilizando métodos audiovisuales para el conocimiento mas simple y mejorado del tema propuesto.
CAÍDA LIBRE

CAÍDA LIBRE

En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquial mente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción des aceleradora de la gravedad, como un disparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin ni de paracaídas durante un cierto trayecto
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la velocidad aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:
(1), son la aceleración y la velocidad verticales.
, es la fuerza de rozamiento fluido dinámicoe aumenta con la velocidad).
- Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial () para las velocidades y la altura vienen dada por:
(2)
- Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluido dinámica que suele ser movilizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico kw:
(3)
- Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:
, es el área transversal a la dirección del movimiento.
, es la densidad del fluido.
, es el signo de la velocidad.
, es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo.
donde:
donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.
En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial ():
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
Donde:
La velocidad límite puede calcularse fácilmente poniendo igual a cero la aceleración en la ecuación ():
La solución analítica de la ecuación diferencial () depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube o para uno que cae. La solución de velocidades para ambos casos es:
Donde:  .
.
 .
.
Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura  y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial
y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial 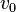 se obtienen los siguientes resultados para la altura del cuerpo:
se obtienen los siguientes resultados para la altura del cuerpo:
 y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial
y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial 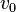 se obtienen los siguientes resultados para la altura del cuerpo:
se obtienen los siguientes resultados para la altura del cuerpo:
Caída libre ( y
y  ):
):
 y
y  ):
):
El tiempo transcurrido en la caída desde la altura  hasta la altura
hasta la altura 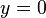 puede obtenerse al reordenar la ecuación anterior:
puede obtenerse al reordenar la ecuación anterior:
 hasta la altura
hasta la altura 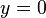 puede obtenerse al reordenar la ecuación anterior:
puede obtenerse al reordenar la ecuación anterior:
Lanzamiento vertical ( y
y 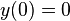 ):
):
 y
y 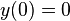 ):
):
Si la altura  es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura  puede calcularse como:
puede calcularse como:
 es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura  puede calcularse como:
puede calcularse como:
Se puede demostrar que el tiempo que tarda un cuerpo en caer desde una altura  hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de  si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
 hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de  si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
sabiendo que  y que
y que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](https://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
 y que
y que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](https://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
Intuitivamente la diferencia de tiempos es clara, en el tiro hacia arriba la velocidad inicial es mayor por lo que la fuerza de rozamiento promedio a lo largo de la trayectoria también es mayor que la que se alcanza en tiro hacia abajo.
MOVIMIENTO PARABÓLICO
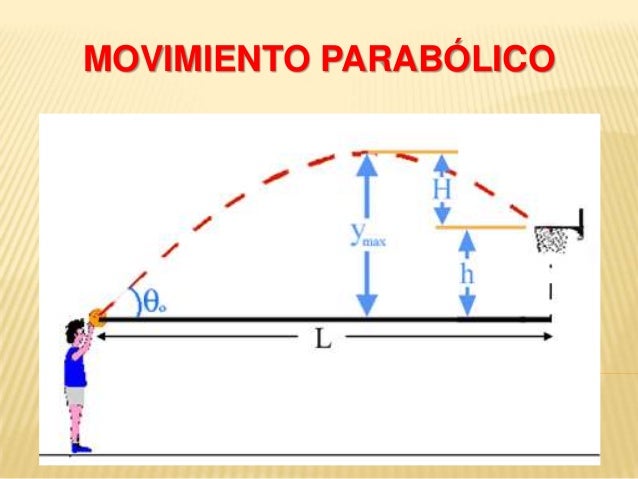
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales).
El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales.
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
- Se puede analizar el movimiento en vertical independientemente del horizontal.
 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad. son dos errores (vectores unitarios) en el plano.
son dos errores (vectores unitarios) en el plano.La velocidad inicial se compone de dos partes:
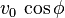 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.En lo sucesivo

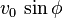 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.En lo sucesivo
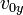
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.
MAPA MENTAL DE MOVIMIENTO PARABÓLICO

VÍDEO EXPLICATIVO DEL MOVIMIENTO
PARABÓLICO
otras actividades
<








![y(t)=h_0-\cfrac{1}{{\alpha}}\ln\left[\cosh\left(-t\sqrt{{\alpha}{g}}\right) \right]](https://upload.wikimedia.org/math/6/4/4/64407f2d5c666902f084e7350c123773.png)

![y(t)=\cfrac{1}{{\alpha}}\ln\left[\cfrac{\cos\left[-t\sqrt{{\alpha}{g}}+\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]}{\cos\left[\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]} \right]](https://upload.wikimedia.org/math/1/6/2/162a803c65007695a5634885c3c8cce0.png)








No hay comentarios.:
Publicar un comentario